Introduction to R: Part One

To learn everything there is to know about R, read the docs. To learn just enough to be dangerous, follow along :)

Introductions and Overview

This workshop serves as a gentle introduction to programming with R, with a focus on application to data science and research. We will cover the basics of R, such as using the command line as a calculator, working with variables, simple data structures, and data types. We will show how to load data sets into R, and how to summarize data with statistics and plots. At the end we will also discuss some considerations when choosing R over other programming languages like Python or SPSS.

Opening the R command line

• The R command line interface (CLI) is a simple interface for entering R commands
• A command is a way of giving the computer some information and having it perform a task

Open in Windows

• start menu (see video below)
• desktop shortcut
• task bar shortcut

Open in Linux

• application menu
• dock shortcut
• terminal (see video below)

Using the console as a calculator

Basic arithmetic operators

Operator	Description	Example
+	addition	3 + 4 = 7
-	subtraction	10 - 2 = 8
*	multiplication	2.5 * 4 = 10
/	division	9 / 2 = 4.5
^	exponentiation	11^2 = 121
%%	modulus	5 %% 3 = 2
%/%	integer division	9 %/% 2 = 4

# Order of operations still applies
5 - 4 + 5*2^4

## [1] 81

# Use parentheses to ensure desired order of operations
(-2 + (5 / 3.8)) * 1.618^2

## [1] -1.791211

Three basic types of numbers

I say there are three types of numbers in R because R has different ways of working with different numbers

Number type	Description	Example
Integer	Whole numbers, positive or negative	4L, -3L, 0L
Decimal	Any number, positive or negative, with a fractional part	3.1, pi, 4.0
Complex	A real decimal number with an imaginary decimal part	-2.1+5i

Notice that the integers have an L at the end. This is to explicitly tell R to represent a number as a [long] integer, rather than a double (decimal) number.

is.integer(4)  # FALSE

## [1] FALSE

is.double(4)   # TRUE

## [1] TRUE

is.integer(4L) # TRUE

## [1] TRUE

Logical operators

Logical operators test for a condition. They ask a question, and the answer is either TRUE or FALSE.

Operator	Description	Example
<	less than	5 < 4 -> FALSE
<=	less than or equal	6 <= 6 -> TRUE
>	greater than	Inf > 1e6 -> TRUE
>=	greater than or equal	3.5 >= 9 -> FALSE
==	exactly equal	sin(0) == 0 -> TRUE
!=	not equal	(3+1)^2 != 3^2 + 1^1 -> TRUE
!	not	!TRUE -> FALSE
&&	and (short-circuiting)	(5 < 7) && (7 < 10) -> TRUE
`		`
&	and (vectorized)	TRUE & 2 > c(1,2,3) -> c(FALSE, FALSE, TRUE)
`	`	or (vectorized)

Other math functions

Function	Description	Example
abs	absolute value of a number	abs(-2.5), abs(3L), abs(3+4i)
sqrt	square root of a number	sqrt(0.81), sqrt(-1+0i)
exp	\(e^x\)	exp(1) -> 2.7182818
log	logarithm of a number (base is the natural number \(e\) by default)
log10	base 10 logarithm of a number (see also log2, log1p, logb)
sin, cos, tan	basic trigonometric functions (radians by default)
asin, acos, atan	inverse trigonometric functions
sinh, asinh, etc.	hyperbolic and inverse hyperbolic trigonometric functions
ceiling	rounds a number towards infinity	ceiling(-2.8) -> -2
floor	rounds a number towards negative infinity	floor(3.9) -> 3
round	rounds a number to a specified number of digits (round to even by default)
trunc	strips the decimal part from a number	trunc(2.1) -> 2, trunc(2.9) -> 2

Also note, all infix operations can be used with prefix notation:

3 + 4 # infix

## [1] 7

`+`(3, 4) # prefix

## [1] 7

Built-in constants and other values

Keyword	Description	Example
Inf	The floating point representation of infinity	1 / 0 -> Inf
-Inf	Negative infinity	1 / -0 -> -Inf
NaN	Not a Number	0 / 0 -> NaN
NA	A placeholder for missing values
NULL	An R object representing the empty set or nothing
pi	The ratio of a circle’s circumference to its diameter	3.14159...

The Institute of Electrical and Electronics Engineers (IEEE, “eye-triple-ee”) sets many of the standards for computer protocol, including how floating point numbers behave. A floating point number is the computer representation of a real number, but due to finite precision, there are some inconsistencies:

0.3 - 0.1 # should be 0.2

## [1] 0.2

(0.3 - 0.1) == 0.2 # should be true

## [1] FALSE

# R is lying to us!
print(0.3-0.1, digits = 20)

## [1] 0.19999999999999998335

# use `all.equal` to test floating point equality
all.equal(0.3 - 0.1, 0.2)

## [1] TRUE

• R uses 64 bit (double) precision for floating point numbers and 32 bit signed integers
• https://en.wikipedia.org/wiki/IEEE_754
• https://en.wikipedia.org/wiki/Division_by_zero#Computer_arithmetic

Practice

The quadratic equation is used to find the roots of quadratic (2nd degree) polynomials. For a quadratic polynomial given by

\[ ax^2 + bx + c \]

the roots are given by

\[ x_{1,2} = \frac{-b \pm \sqrt{b^2 -4ac}}{2a} \]

Find the roots of the following equations using the quadratic equation:

1. \(y = 2x^2 + 2x - 24\)
2. \(y = 4x^2 + 9\)
3. \(y = x^2 + 4x + 4\)

Accessing the built-in docs

Most if not all functions in R have useful help documentation that can be accessed directly within the R console.

> help(sum)

> ?sum

> library(help = "base")

Working with variables

• Let you store a number or other object in the environment list
• Similar to “memory recall” of a calculator, but better

To create a new variable, we can use left or right assignment:

# left assignment
x <- 10
# right assignment
"some string" -> y

• You can use an “equal sign” for assignment, but it is discouraged

To list all variables in the session (environment), do:

# list all variables in the environment
ls()

##  [1] "cols"            "ends"            "names"           "read_fwf2"      
##  [5] "starts"          "values"          "weather_raw"     "weather_rawTest"
##  [9] "x"               "y"

We can see what is stored in those variables by typing them into the console:

# show what is stored in the variables
x

## [1] 10

y

## [1] "some string"

Good variable naming conventions (in R)

• See the tidyverse style guide for a full rundown of object naming
• let your names be meaningful
• let your names be consistent
• avoid using existing function names (e.g. mean, c) and objects (e.g. T, F, pi)
  • List of reserved words in R: https://cran.r-project.org/doc/manuals/R-lang.html#Reserved-words
• avoid using dots
• use the existing conventions of whatever project you are contributing to

Basic data types in R

# logical (boolean)
typeof(TRUE)

## [1] "logical"

# integer
typeof(5L) # note the 'L' at the end

## [1] "integer"

# double
typeof(6.3)

## [1] "double"

typeof(4) # no 'L' at the end --> double

## [1] "double"

# complex
typeof(3 + 2i)

## [1] "complex"

# character
typeof("hello world")

## [1] "character"

Working with different data types

Coercion and conversion

• R will always coerce (convert) an object to the least restrictive type

typeof(TRUE + 3L)

## [1] "integer"

typeof(TRUE + 3.0)

## [1] "double"

typeof(TRUE + 3 + 0i)

## [1] "complex"

Guess the output type

# a "regular" number
14

## [1] 14

# integer division
14 %/% 3

## [1] 4

# remainder
14 %% 3

## [1] 2

# ceiling/floor/round
ceiling(pi)

## [1] 4

round(pi)

## [1] 3

How can we ensure the output type of an operation? Most of the time it’s okay to let R worry about the return types. In other situations, there’s the as command:

as.integer(4.0)

## [1] 4

as.logical(4L) # any non-zero value is true

## [1] TRUE

as.complex(4)

## [1] 4+0i

as.double("3.14159")

## [1] 3.14159

Careful, as not every value can be coerced to every other type, or no robust checks will be performed to ensure validity of a conversion:

# converts to an integer via truncation
as.integer(4.5)

## [1] 4

Testing for types

We can use the is command to ask R what the type of an object is:

is.integer(4L)

## [1] TRUE

is.double(3+2i)

## [1] FALSE

is.numeric(4)

## [1] TRUE

is.numeric(4L)

## [1] TRUE

is.numeric(4+2i)

## [1] FALSE

Sometimes a thing that looks like an integer is really a double:

# actually a double
x <- 4
is.integer(x)

## [1] FALSE

How to check that a number is an integer:

as.integer(x) == x

## [1] TRUE

Special data type: Factors

A factor looks like a string, but acts like an integer (most of the time).

# most often used for categorical observations
pets <- c("cat", "dog", "lizard", "raccoon")
(pet_obs <- sample(pets, 20, TRUE))

##  [1] "cat"     "raccoon" "lizard"  "cat"     "cat"     "lizard"  "raccoon"
##  [8] "dog"     "dog"     "dog"     "dog"     "cat"     "cat"     "cat"    
## [15] "cat"     "lizard"  "raccoon" "raccoon" "raccoon" "lizard"

# Turn the character vector into a set of factors
pet_fct <- factor(pet_obs)
pet_fct

##  [1] cat     raccoon lizard  cat     cat     lizard  raccoon dog     dog    
## [10] dog     dog     cat     cat     cat     cat     lizard  raccoon raccoon
## [19] raccoon lizard 
## Levels: cat dog lizard raccoon

# can be converted to an integer vector
as.integer(pet_fct)

##  [1] 1 4 3 1 1 3 4 2 2 2 2 1 1 1 1 3 4 4 4 3

# can be converted to a character vector
as.character(pet_fct)

##  [1] "cat"     "raccoon" "lizard"  "cat"     "cat"     "lizard"  "raccoon"
##  [8] "dog"     "dog"     "dog"     "dog"     "cat"     "cat"     "cat"    
## [15] "cat"     "lizard"  "raccoon" "raccoon" "raccoon" "lizard"

Overview of objects and data structures

For a full overview, see the R documentation on basic types.

• Vectors
• Matrices and Arrays
• Lists
• Compound objects
  • Factors
  • Data frames

Working with vectors, matrices, and arrays

Vectors

• a vector is a collection of same-type objects
• aka an atomic vector
• all elements coerced to the least restrictive type
• typically created using the concatenate command, c()

# a few vectors
c(4.5, 2, 3.8)
1:4
c(TRUE, FALSE, FALSE)
seq(from = 0.1, to = 1.0, by = 0.4)
LETTERS

## [1] 4.5 2.0 3.8
## [1] 1 2 3 4
## [1]  TRUE FALSE FALSE
## [1] 0.1 0.5 0.9
##  [1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N" "O" "P" "Q" "R" "S"
## [20] "T" "U" "V" "W" "X" "Y" "Z"

Question: What is meant by “least restrictive type”?

# mix of integer and logical
c(TRUE, 5L, -2L, FALSE)

## [1]  1  5 -2  0

# mix of integer and double
c(5L, pi, -7L, 2.2)

## [1]  5.000000  3.141593 -7.000000  2.200000

# mix of double and complex
c(pi, -2+7i, 6.9, -3.5i)

## [1]  3.141593+0.0i -2.000000+7.0i  6.900000+0.0i  0.000000-3.5i

# mix of double and character
c("asdf", 6.12, pi, "3")

## [1] "asdf"             "6.12"             "3.14159265358979" "3"

We can access the elements of a vector by using brackets: []. Note that R uses “one-based indexing”, meaning that arrays start at \(1\), not \(0\).

# accessing a single element from `letters`
letters[4]

## [1] "d"

# accessing multiple elements using a vector of indices
letters[c(1, 3, 5)]

## [1] "a" "c" "e"

# accessing a subset using conditionals
x <- 1:10
x[x < 4]

## [1] 1 2 3

# accessing the last element
tail(letters, n = 1)

## [1] "z"

letters[length(letters)]

## [1] "z"

Matrices

• A matrix in R is a vector with a dim attribute
• It is stored in memory the same way as a vector is

# creating a matrix using the `matrix()` function
matrix(1:12, nrow = 3, ncol = 4)

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# filling a matrix with a single value
matrix("m", nrow = 5, ncol = 2)

##      [,1] [,2]
## [1,] "m"  "m" 
## [2,] "m"  "m" 
## [3,] "m"  "m" 
## [4,] "m"  "m" 
## [5,] "m"  "m"

Matrices (and vectors and arrays) are stored in column-major order

# default: fills in down each column
matrix(1:12, nrow = 3)

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# explicitly fill in accross rows first
matrix(1:12, nrow = 3, byrow = TRUE)

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

Elements of a matrix can either be accessed with row-column pairs, or with linear indexing

# create a 3x5 matrix
(M <- matrix(1:15, nrow = 3))

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    4    7   10   13
## [2,]    2    5    8   11   14
## [3,]    3    6    9   12   15

# get the element at the second row and fourth column
M[2, 4]

## [1] 11

# get the 8th element in memory
M[8]

## [1] 8

You can create subsets of a matrix using a pair of vectors for indices.

# get rows 1 and 3, and columns 2 and 4
M[c(1, 3), c(2, 4)]

##      [,1] [,2]
## [1,]    4   10
## [2,]    6   12

A matrix can be turned back into a vector by removing its dimension attribute. In the same way, a matrix can be reshaped, or a vector can be turned into a matrix.

# show the attributes of the matrix, M
attributes(M)

## $dim
## [1] 3 5

# get the `dim` attribute
attr(M, "dim")

## [1] 3 5

# remove the `dim` attribute by setting it to `NULL`
attr(M, "dim") <- NULL
M

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15

# turn M into a 5x3 matrix
attr(M, "dim") <- c(5, 3)
M

##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]    2    7   12
## [3,]    3    8   13
## [4,]    4    9   14
## [5,]    5   10   15

Arrays

• An array is an extension of a matrix, having 2 or more dimensions
• Arrays are created using the array() function or by setting the dim attribute of a vector

# one array
(a <- array(1:(5*4*3), dim = c(5, 4, 3)))

## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]    1    6   11   16
## [2,]    2    7   12   17
## [3,]    3    8   13   18
## [4,]    4    9   14   19
## [5,]    5   10   15   20
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,]   21   26   31   36
## [2,]   22   27   32   37
## [3,]   23   28   33   38
## [4,]   24   29   34   39
## [5,]   25   30   35   40
## 
## , , 3
## 
##      [,1] [,2] [,3] [,4]
## [1,]   41   46   51   56
## [2,]   42   47   52   57
## [3,]   43   48   53   58
## [4,]   44   49   54   59
## [5,]   45   50   55   60

# show the attributes
attributes(a)

## $dim
## [1] 5 4 3

Working with lists

• A list is a “generic vector”
• Each element of a list can be any type of R object

(L <- list(a = 1, "d", formula(y ~ x), sublist = list(a = 1, b = 1:4, c = letters[3:7])))

## $a
## [1] 1
## 
## [[2]]
## [1] "d"
## 
## [[3]]
## y ~ x
## 
## $sublist
## $sublist$a
## [1] 1
## 
## $sublist$b
## [1] 1 2 3 4
## 
## $sublist$c
## [1] "c" "d" "e" "f" "g"

As seen above, lists can hold other lists, and elements can be named or referenced by index. This can become complicated to mentally parse as printed above, so the str command can come in handy.

str(L)

## List of 4
##  $ a      : num 1
##  $        : chr "d"
##  $        :Class 'formula'  language y ~ x
##   .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
##  $ sublist:List of 3
##   ..$ a: num 1
##   ..$ b: int [1:4] 1 2 3 4
##   ..$ c: chr [1:5] "c" "d" "e" "f" ...

Elements of a list can be accessed in three different ways.

# Using single bracket notation. Returns a list containing the object at this index.
L[1]

## $a
## [1] 1

# Using the `$` selector. Returns the object at this index.
L$a

## [1] 1

# Using double bracket notation. Returns the object at this index.
L[[1]]

## [1] 1

Working with data frames

What are some of the key properties of a data frame?

• Two dimensional (tabular)
• Can be a mix of numeric, logical, and character (and more) types
• All columns are the same length

A data frame is essentially a list with a few extra restrictions

Accessing elements of a data frame is similar to lists and matrices.

# getting a single column using the `$` selector or `[[`
mtcars$mpg # column "mpg"

##  [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
## [16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
## [31] 15.0 21.4

mtcars[["mpg"]] # column "mpg"

##  [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
## [16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
## [31] 15.0 21.4

# getting multiple columns using `[` and a index/character vector
mtcars["mpg"] # a new data frame with just the "mpg" column

##                      mpg
## Mazda RX4           21.0
## Mazda RX4 Wag       21.0
## Datsun 710          22.8
## Hornet 4 Drive      21.4
## Hornet Sportabout   18.7
## Valiant             18.1
## Duster 360          14.3
## Merc 240D           24.4
## Merc 230            22.8
## Merc 280            19.2
## Merc 280C           17.8
## Merc 450SE          16.4
## Merc 450SL          17.3
## Merc 450SLC         15.2
## Cadillac Fleetwood  10.4
## Lincoln Continental 10.4
## Chrysler Imperial   14.7
## Fiat 128            32.4
## Honda Civic         30.4
## Toyota Corolla      33.9
## Toyota Corona       21.5
## Dodge Challenger    15.5
## AMC Javelin         15.2
## Camaro Z28          13.3
## Pontiac Firebird    19.2
## Fiat X1-9           27.3
## Porsche 914-2       26.0
## Lotus Europa        30.4
## Ford Pantera L      15.8
## Ferrari Dino        19.7
## Maserati Bora       15.0
## Volvo 142E          21.4

mtcars[1:3] # columns 1 through 3

##                      mpg cyl  disp
## Mazda RX4           21.0   6 160.0
## Mazda RX4 Wag       21.0   6 160.0
## Datsun 710          22.8   4 108.0
## Hornet 4 Drive      21.4   6 258.0
## Hornet Sportabout   18.7   8 360.0
## Valiant             18.1   6 225.0
## Duster 360          14.3   8 360.0
## Merc 240D           24.4   4 146.7
## Merc 230            22.8   4 140.8
## Merc 280            19.2   6 167.6
## Merc 280C           17.8   6 167.6
## Merc 450SE          16.4   8 275.8
## Merc 450SL          17.3   8 275.8
## Merc 450SLC         15.2   8 275.8
## Cadillac Fleetwood  10.4   8 472.0
## Lincoln Continental 10.4   8 460.0
## Chrysler Imperial   14.7   8 440.0
## Fiat 128            32.4   4  78.7
## Honda Civic         30.4   4  75.7
## Toyota Corolla      33.9   4  71.1
## Toyota Corona       21.5   4 120.1
## Dodge Challenger    15.5   8 318.0
## AMC Javelin         15.2   8 304.0
## Camaro Z28          13.3   8 350.0
## Pontiac Firebird    19.2   8 400.0
## Fiat X1-9           27.3   4  79.0
## Porsche 914-2       26.0   4 120.3
## Lotus Europa        30.4   4  95.1
## Ford Pantera L      15.8   8 351.0
## Ferrari Dino        19.7   6 145.0
## Maserati Bora       15.0   8 301.0
## Volvo 142E          21.4   4 121.0

# getting a single element using `[`
mtcars[1, 3] # row 1, col 3 ("disp")

## [1] 160

# getting a single element using `$` and `[`
mtcars$disp[1] # row 1, col 3 ("disp")

## [1] 160

Reading data from a file

Common text files can be read using the read- set of functions

• read comma separated values (CSV) files with read.csv()
  • the more general function is read.delim()
  • the other specialized function is read.table()
• read general text files using readLines()

# read in the sample csv file
df <- read.csv("data/simple_csv.csv")
df

##                      X  mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## 1            Mazda RX4 21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
## 2        Mazda RX4 Wag 21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
## 3           Datsun 710 22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## 4       Hornet 4 Drive 21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
## 5    Hornet Sportabout 18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
## 6              Valiant 18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
## 7           Duster 360 14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
## 8            Merc 240D 24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## 9             Merc 230 22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## 10            Merc 280 19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
## 11           Merc 280C 17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
## 12          Merc 450SE 16.4   8 275.8 180 3.07 4.070 17.40  0  0    3    3
## 13          Merc 450SL 17.3   8 275.8 180 3.07 3.730 17.60  0  0    3    3
## 14         Merc 450SLC 15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
## 15  Cadillac Fleetwood 10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
## 16 Lincoln Continental 10.4   8 460.0 215 3.00 5.424 17.82  0  0    3    4
## 17   Chrysler Imperial 14.7   8 440.0 230 3.23 5.345 17.42  0  0    3    4
## 18            Fiat 128 32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## 19         Honda Civic 30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## 20      Toyota Corolla 33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## 21       Toyota Corona 21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## 22    Dodge Challenger 15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
## 23         AMC Javelin 15.2   8 304.0 150 3.15 3.435 17.30  0  0    3    2
## 24          Camaro Z28 13.3   8 350.0 245 3.73 3.840 15.41  0  0    3    4
## 25    Pontiac Firebird 19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2
## 26           Fiat X1-9 27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## 27       Porsche 914-2 26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## 28        Lotus Europa 30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## 29      Ford Pantera L 15.8   8 351.0 264 4.22 3.170 14.50  0  1    5    4
## 30        Ferrari Dino 19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6
## 31       Maserati Bora 15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
## 32          Volvo 142E 21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

More proprietary formats can be read in using a library

• readr for the tidyverse version of read- functions
• readxl for Excel spreadsheets
• R.matlab for Matlab files

Fitting a linear model

R has built-in support for fitting \[generalized\] linear models, with support for numeric and factor variables.

# y ~ normal(3x + 2, 0.5)
x <- rnorm(30)
y <- rnorm(length(x), 3*x + 2, 0.5)
plot(y ~ x) # same as plot(x, y)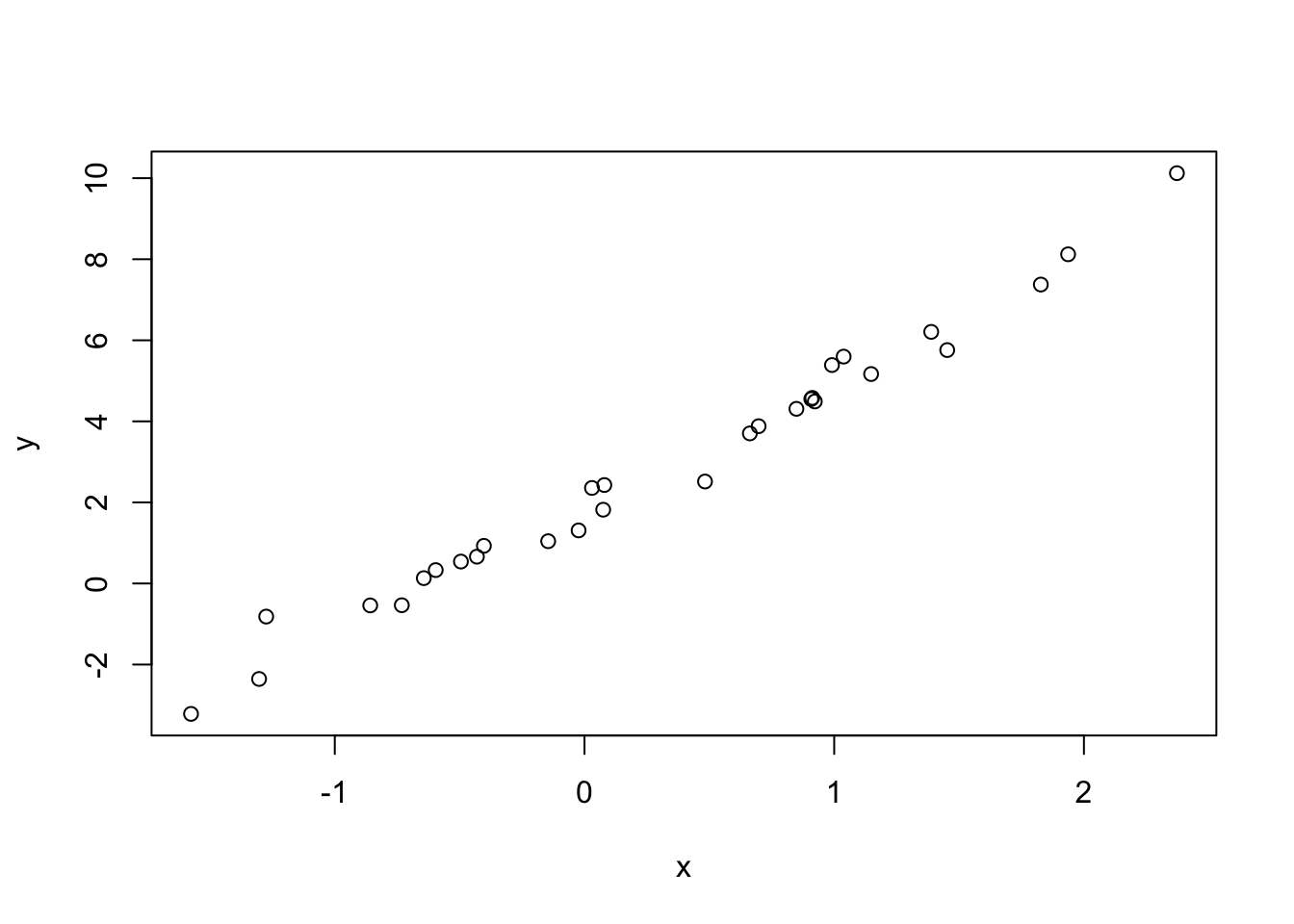

# fit a linear model
lm(y ~ x) # slope-intercept model. Same as `lm(y ~ 1 + x)`

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##       1.913        3.063

lm(y ~ 0 + x) # slope only model (no intercept)

## 
## Call:
## lm(formula = y ~ 0 + x)
## 
## Coefficients:
##     x  
## 3.601

Can also fit a generalized linear model using (you guessed it) the glm() function.

# logit(theta) = 3x + 2
k <- rbinom(length(x), size = 1, prob = plogis(3*x+2))
plot(k ~ x)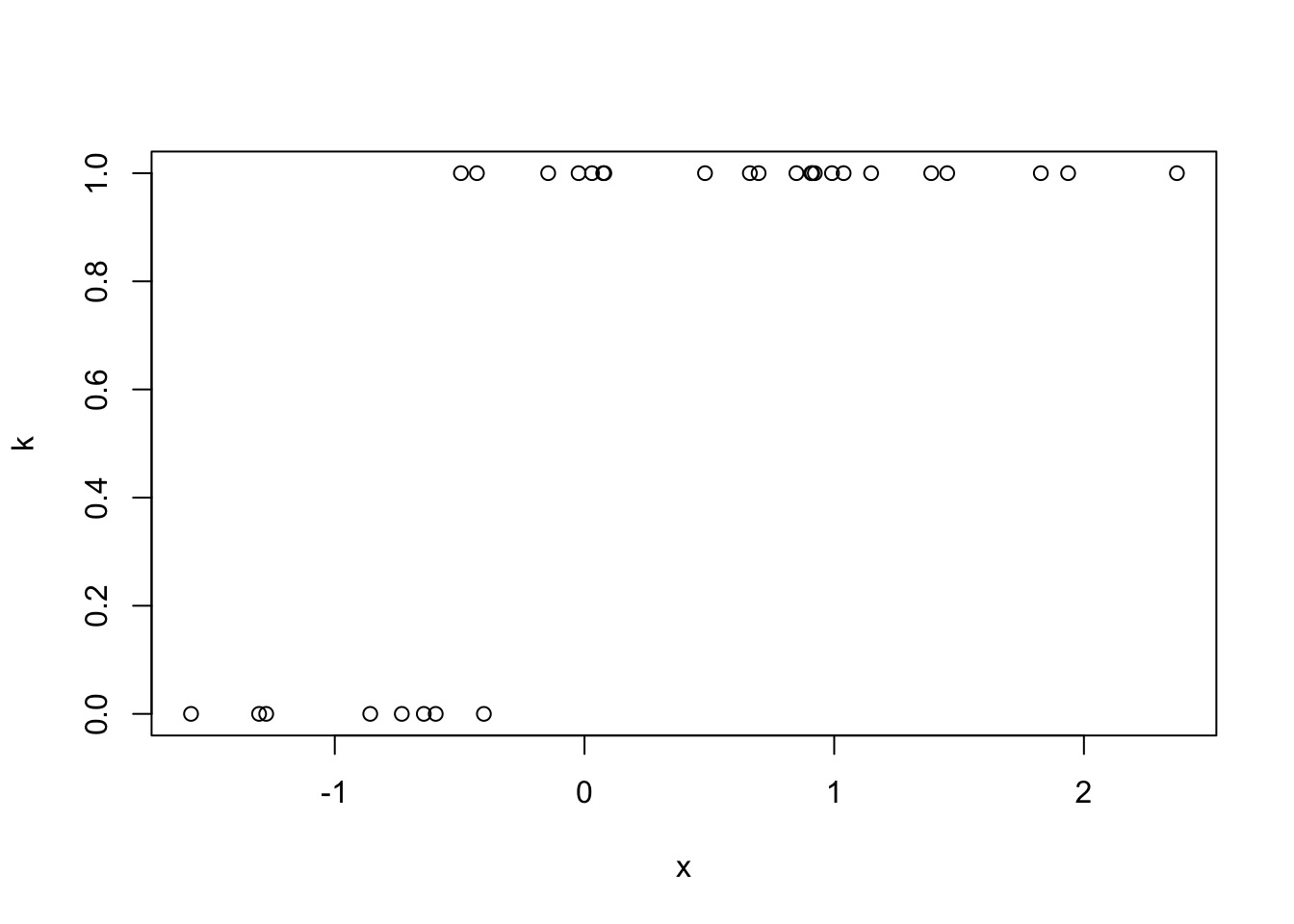

# fit a generalized linear model with logit link
glm(k ~ 1 + x, family = binomial(link = "logit"))

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## 
## Call:  glm(formula = k ~ 1 + x, family = binomial(link = "logit"))
## 
## Coefficients:
## (Intercept)            x  
##       6.442       13.736  
## 
## Degrees of Freedom: 29 Total (i.e. Null);  28 Residual
## Null Deviance:       34.79 
## Residual Deviance: 5.789     AIC: 9.789

Summarizing data frames and models

R has a method for summarizing vectors, data frames, and fitted models, and it is the summary() function.

# summarize a numeric vector
z <- rnorm(50)
summary(z)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -1.99734 -0.63997  0.05107 -0.05718  0.39949  1.39176

# summarize a data frame
df <- data.frame(a = 1L:10L, b = rexp(10), c = factor(sample(c("a", "b", "c"), 10, TRUE)))
summary(df)

##        a               b          c    
##  Min.   : 1.00   Min.   :0.5054   b:7  
##  1st Qu.: 3.25   1st Qu.:0.7583   c:3  
##  Median : 5.50   Median :0.9356        
##  Mean   : 5.50   Mean   :1.3481        
##  3rd Qu.: 7.75   3rd Qu.:1.3709        
##  Max.   :10.00   Max.   :3.3454

# summarize a linear model
fit <- lm(y ~ 1 + x)
summary(fit)

## 
## Call:
## lm(formula = y ~ 1 + x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.8755 -0.2574 -0.1310  0.2476  1.1738 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.91324    0.08416   22.73   <2e-16 ***
## x            3.06252    0.08026   38.16   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4404 on 28 degrees of freedom
## Multiple R-squared:  0.9811, Adjusted R-squared:  0.9805 
## F-statistic:  1456 on 1 and 28 DF,  p-value: < 2.2e-16

Notice that it outputs differently for different input objects. This is because summary() is a generic function, meaning that it has multiple methods defined for different R objects, and packages can define their own behavior for their own types.

Producing simple plots

There are a few simple plotting functions in R

• plot()
  • also “generic”
  • can produce scatter and line plots
• lines() adds lines to plots
• points() adds points to plots
• curve() plots a function over a domain
  • can be used alone or “layered” on top of an existing plot

Other types of graphs include

• hist() for histograms
• barplot()
• boxplot()
• stem() for stem-and-leaf plot